Newton-Raphson Method

This method is generally used to improve the result obtained by one of the previous methods. Let x_o be an approximate root of f(x) = 0 and let x₁ = x_o + h be the correct root so that f(x₁) = 0. Expanding f(x_o + h) by Taylor’s series, we obtain

f(x_o) + hf’(x_o) + h²f’’(x_o)/2! +-----= 0

Neglecting the second and higher order derivatives, we have

f(x_o) + hf’(x_o) = 0

Which gives

h = - f(x_o)/f’(x_o)

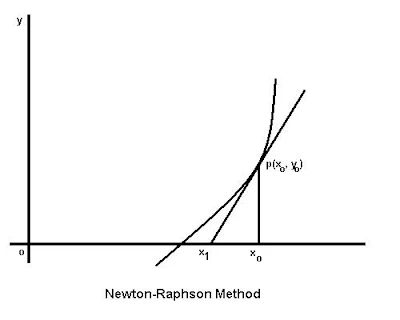
A better approximation than x_o is therefore given be x₁, where

x₁ = x_o– f(x_o)/f’(x_o)

Successive approximations are given by x₂, x₃,----,x_n+1, where

x_n+1= x_n – f(x_n)/f’(x_n)

Which is the Newton-Raphson formula.

Example: - Find a real root of the equation x³ -5x + 3 = 0.

Solⁿ: -

Let, f(x) = x³ -5x + 3 = 0

f’(x) = 3x² - 5

Choosing x_o = 1

Step-1:

f(x_o) = -1

f(x_o) = -2

So, x₁ =1 – ½ = 0.5

Step-2:

f(x₁) = 0.625

f’(x₁) = -4.25

x₂ = 0.5 + 0.625/4.25 = 0.647

Step-3:

f(x₂) = 0.0356

f’(x₂) = -4.139

X3 = 0.647+ 0.0356/4.1393 = 0.6556

Step-4:

f(x₃) = 0.0037

f’(x₃) = -3.7105

x₄ = 0.6556 + 0.0037/3.7105 = 0.6565

The successive approximation 0.6565

Comments

Runge-Kutta-Fehlberg Method

One way to guarantee accuracy in the solution of an I.V.P. is to solve the problem twice using step sizes h and and compare answers at the mesh points corresponding to the larger step size. But this requires a significant amount of computation for the smaller step size and must be repeated if it is determined that the agreement is not good enough. The Runge-Kutta-Fehlberg method (denoted RKF45) is one way to try to resolve this problem. It has a procedure to determine if the proper step size h is being used. At each step, two different approximations for the solution are made and compared. If the two answers are in close agreement, the approximation is accepted. If the two answers do not agree to a specified accuracy, the step size is reduced. If the answers agree to more significant digits than required, the step size is increased. Each Runge-Kutta-Fehlberg step requires the use of the following six values: Then an approximation to the solution of the I.V.P....

Van Der Pol System

The van der Pol equation is an ordinary differential equation that can be derived from the Rayleigh differential equation by differentiating and setting . It is an equation describing self-sustaining oscillations in which energy is fed into small oscillations and removed from large oscillations. This equation arises in the study of circuits containing vacuum tubes and is given by If , the equation reduces to the equation of simple harmonic motion The van der Pol equation is , where is a constant. When the equation reduces to , and has the familiar solution . Usually the term in equation (1) should be regarded as friction or resistance, and this is the case when the coefficient is positive. However, if the coefficient is negative then we have the case of "negative resistance." In the age of "vacuum tube" radios, the " tetrode vacuum tube " (cathode, grid, plate), was used for a power amplifie...

Powell's Method

The essence of Powell's method is to add two steps to the process described in the preceding paragraph. The vector represents, in some sense, the average direction moved over the n intermediate steps in an iteration. Thus the point is determined to be the point at which the minimum of the function f occurs along the vector . As before, f is a function of one variable along this vector and the minimization could be accomplished with an application of the golden ratio or Fibonacci searches. Finally, since the vector was such a good direction, it replaces one of the direction vectors for the next iteration. The iteration is then repeated using the new set of direction vectors to generate a sequence of points . In one step of the iteration instead of a zig-zag path the iteration follows a "dog-leg" path. The process is outlined below. Let be an initial guess at the location of the minimum of the function . Let for be the ...

Numerical Analysis

Search This Blog